Introduction
Angles are an essential component of geometry. They are used to measure the amount of rotation between two rays or line segments. Whether you are a student studying geometry or just someone who is curious about how to measure angles, this article will provide you with the basics of angle measurement, including how to use a protractor and solve for missing angles.
Basic Explanation and Formulas
An angle is formed when two rays or line segments share a common endpoint. The vertex of the angle is the shared endpoint, and the rays or line segments are called the angle’s sides. Each angle has a measure associated with it, which corresponds to the amount of rotation between the two sides.
The unit of measurement for angles is degrees, and there are 360 degrees in a complete circle. There are a few different formulas that can be used to find the measure of an angle, but the most common one is:
Measure of Angle = Arc Length / Radius
In this formula, the arc length is the length of the arc that forms the angle, and the radius is the distance from the center of the circle to the endpoint of the arc.
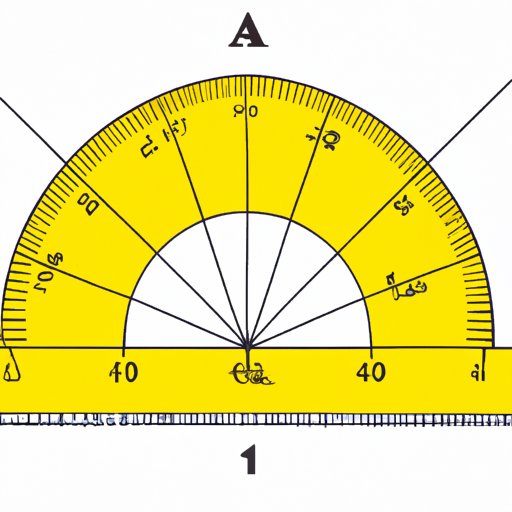
Measuring Angles with a Protractor
A protractor is a tool used for measuring angles. It consists of a semicircular shape with degree markings along the curved edge and a straight edge that connects to the midpoint of the curve. Here are the steps to measure an angle with a protractor:
- Place the midpoint of the straight edge of the protractor over the vertex of the angle.
- Align one of the sides of the angle with the straight edge of the protractor.
- Read the degree measurement where the other side of the angle intersects with the curved edge of the protractor.
Here is an example of how to use a protractor to measure an angle:

In this example, the measure of the angle is 110 degrees.
Solving for Missing Angles
Sometimes, you may need to find the measure of an angle that is not directly given to you. In these cases, you can use what you know about angles to solve for the missing measure. Here is an example of how to solve for a missing angle:
If angle A measures 25 degrees and angle B is a straight angle, what is the measure of angle C?
To solve for the missing angle, we can use the fact that the angles in a triangle add up to 180 degrees. In this case, we know the measures of two of the angles, so we can solve for the third:
Angle A + Angle B + Angle C = 180 degrees
Therefore, 25 degrees + 180 degrees + Angle C = 180 degrees
Subtracting 25 from each side gives us:
Angle C = 155 degrees
Common Angle Types
There are five common types of angles that you should know:
- Acute Angle: An angle that measures less than 90 degrees.
- Right Angle: An angle that measures exactly 90 degrees.
- Obtuse Angle: An angle that measures more than 90 degrees but less than 180 degrees.
- Straight Angle: An angle that measures exactly 180 degrees.
- Reflex Angle: An angle that measures more than 180 degrees but less than 360 degrees.
Here is an example of each angle type:

Practice Problems
Work through these practice problems to test your understanding of angle measurement:
- What is the measure of a straight angle?
- What is the measure of an obtuse angle?
- What is the measure of the missing angle in this triangle: angle A = 30 degrees, angle B = 60 degrees?
- What is the measure of a reflex angle?
- Using a protractor, measure the angle formed by the two lines below. Round your answer to the nearest whole number.

Answers:
- 180 degrees
- Any angle greater than 90 degrees but less than 180 degrees
- 90 degrees
- Any angle greater than 180 degrees but less than 360 degrees
- 100 degrees
Visual Aids
Throughout the article, diagrams, pictures, and graphs have been included to help you understand the concepts. Here are a few examples:

Real-World Applications
Angle measurement is a crucial component of numerous fields, including engineering, construction, and map-making. In these fields, precise angle measurements are necessary to ensure building and roadway construction is accurate and mapping is correct. Without proper angle measurements, these structures could be unstable or, in the case of mapping, misrepresent the landscape they depict.
For instance, in the field of engineering, angles are used to calculate the angles of support structures like trusses and diagonal braces for buildings, bridges, or towers. So, knowing the ability to calculate the angle to ensure that the support structure can bear weight and withstand forces such as wind, rain, and earthquakes.
Conclusion
Knowing how to measure angles and solve for missing angles is an essential tool for anyone studying geometry or interested in how angles are used in various real-world contexts. Using a protractor is a simple way to measure angles, but understanding the basic formulas for measuring angles will provide you with a deeper understanding of the mathematical concepts that underpin angle measurement.
Remember to study common angle types and their properties, work through practice problems, and pay attention to the visual aids provided throughout the article. Applying the knowledge you have gained from this article will allow you to better understand geometry and apply it in various real-world settings.




